せっかく剛体の運動方程式と姿勢の表現が手に入ったので，数値計算をして運動を視覚化するところまでやってみよう．ポテンシャルや拘束がなく，剛体1つが運動しているものとする．このとき，並進運動は質点の運動と変わらないので，今回は回転運動だけに注目しよう．何もない空間で，ものがぐるぐる回転しているような状況をイメージすればよい．
ルンゲクッタ法
回転運動のシミュレーションをするには，運動方程式と姿勢の微分方程式の2つを更新していかなければならないので，大まかな計算の流れは次の図のようになる．
今回は，ルンゲクッタ法を用いて時間発展させる．ルンゲクッタ法に関するもう少し詳しい説明は別記事（ルンゲクッタ法の精度確認）を見てもらいたい．実際の計算上では，ルンゲクッタ法を適用するため，運動方程式と姿勢の微分方程式を同時に積分するような形になっている．座標の基底ベクトルを用いた場合の更新式は以下の通りだ．
Pythonによるコーディング例
これをPythonでコーディングしてみた一例を以下に示しておく．姿勢の更新にクオータニオンを用いた場合と座標の基底ベクトル（DCM）を用いた場合，両方の関数を用意してみた．
import numpy as np
def skew(vec):
# create a skew symmetric matrix from a vector
mat = np.array([[0, -vec[2], vec[1]],
[vec[2], 0, -vec[0]],
[-vec[1], vec[0], 0]])
return mat
# convert an inertia around CoG
def inertia_conversion(mass, inertia, cog):
mat = np.array([[cog[0]*cog[0], cog[0]*cog[1], cog[0]*cog[2]],
[cog[1]*cog[0], cog[1]*cog[1], cog[1]*cog[2]],
[cog[2]*cog[0], cog[2]*cog[1], cog[2]*cog[2]]])
inertia_cog = inertia - mass * (np.dot(cog,cog)*np.identity(3) - mat)
return inertia_cog
def dcm2euler(dcm):
# calculate 321 Euler angles [rad] from DCM
sin_theta = - dcm[0,2]
if sin_theta == 1 or sin_theta == -1:
theta = np.arcsin(sin_theta)
psi = 0
sin_phi = -dcm(2,1)
phi = np.arcsin(sin_phi)
else:
theta = np.arcsin(sin_theta)
phi = np.arctan2(dcm[1,2], dcm[2,2])
psi = np.arctan2(dcm[0,1], dcm[0,0])
euler = np.array([psi, theta, phi])
return euler
def dcm2quaternion(dcm):
# calculate quaternion from DCM
q = np.zeros(4, dtype=float)
q[3] = 0.5 * np.sqrt(1 + dcm[0,0] + dcm[1,1] + dcm[2,2])
q[0] = 0.25 * (dcm[1,2] - dcm[2,1]) / q[3]
q[1] = 0.25 * (dcm[2,0] - dcm[0,2]) / q[3]
q[2] = 0.25 * (dcm[0,1] - dcm[1,0]) / q[3]
return q
def euler2dcm(euler):
phi = euler[0] # Z axis Yaw
theta = euler[1] # Y axis Pitch
psi = euler[2] # X axis Roll
rotx = np.array([[1, 0, 0],
[0, np.cos(psi), np.sin(psi)],
[0, -np.sin(psi), np.cos(psi)]])
roty = np.array([np.cos(theta), 0, -np.sin(theta)],
[0, 1, 0],
[np.sin(theta), 0, np.cos(theta)])
rotz = np.array([[np.cos(phi), np.sin(phi), 0],
[-np.sin(phi), np.cos(phi), 0],
[0, 0, 1]])
dcm = rotx @ roty @ rotz
return dcm
# calculate DCM from quaternion
def quaternion2dcm(q):
dcm = np.zeros((3,3), dtype=float)
dcm[0,0] = q[0]*q[0] - q[1]*q[1] - q[2]*q[2] + q[3]*q[3]
dcm[0,1] = 2 * (q[0]*q[1] + q[2]*q[3])
dcm[0,2] = 2 * (q[0]*q[2] - q[1]*q[3])
dcm[1,0] = 2 * (q[0]*q[1] - q[2]*q[3])
dcm[1,1] = - q[0]*q[0] + q[1]*q[1] - q[2]*q[2] + q[3]*q[3]
dcm[1,2] = 2 * (q[1]*q[2] + q[0]*q[3])
dcm[2,0] = 2 * (q[0]*q[2] + q[1]*q[3])
dcm[2,1] = 2 * (q[1]*q[2] - q[0]*q[3])
dcm[2,2] = - q[0]*q[0] - q[1]*q[1] + q[2]*q[2] + q[3]*q[3]
return dcm
# differential calculation of the body fixed frame
def coordinate_differential(omega, frame_T):
ddt_frame = skew(frame_T @ omega) @ frame_T
return ddt_frame
# differential calculation of omega
def omega_differential(omega, inertia_cog, inertia_inv):
ddt_omega = - inertia_inv @ np.cross(omega, inertia_cog @ omega)
return ddt_omega
# differntial calculation of quaternion
def quaternion_differential(omega, quaternion):
mat = np.array([[0, omega[2], -omega[1], omega[0]],
[-omega[2], 0, omega[0], omega[1]],
[ omega[1], -omega[0], 0, omega[2]],
[-omega[0], -omega[1], -omega[2], 0]])
ddt_quaternion = 0.5 * mat @ quaternion
return ddt_quaternion
# one step itegration
def runge_kutta(omega_b, frame_b, inertia_cog, inertia_inv, dt):
k1 = omega_differential(omega_b, inertia_cog, inertia_inv)
k2 = omega_differential(omega_b + 0.5*dt*k1, inertia_cog, inertia_inv)
k3 = omega_differential(omega_b + 0.5*dt*k2, inertia_cog, inertia_inv)
k4 = omega_differential(omega_b + dt*k3, inertia_cog, inertia_inv)
l1 = coordinate_differential(omega_b, frame_b)
l2 = coordinate_differential(omega_b + 0.5*dt*k1, frame_b + 0.5*dt*l1)
l3 = coordinate_differential(omega_b + 0.5*dt*k2, frame_b + 0.5*dt*l2)
l3 = coordinate_differential(omega_b + dt*k3, frame_b + dt*l3)
new_omega_b = omega_b + 1/6 * (k1 + 2*k2 + 2*k3 + k4) * dt
new_frame_b = frame_b + 1/6 * (l1 + 2*l2 + 2*l3 + l4) * dt
new_frame_b[:,0] = new_frame_b[:,0] / np.linalg.norm(new_frame_b[:,0])
new_frame_b[:,1] = new_frame_b[:,1] / np.linalg.norm(new_frame_b[:,1])
new_frame_b[:,2] = new_frame_b[:,2] / np.linalg.norm(new_frame_b[:,2])
return new_omega_b, new_frame_b
def runge_kutta_quaternion(omega_b, quaternion, inertia_cog, inertia_inv, dt):
k1 = omega_differential(omega_b, inertia_cog, inertia_inv)
k2 = omega_differential(omega_b + 0.5*dt*k1, inertia_cog, inertia_inv)
k3 = omega_differential(omega_b + 0.5*dt*k2, inertia_cog, inertia_inv)
k4 = omega_differential(omega_b + dt*k3, inertia_cog, inertia_inv)
l1 = quaternion_differential(omega_b, quaternion)
l2 = quaternion_differential(omega_b + 0.5*dt*k1, quaternion + 0.5*dt*l1)
l3 = quaternion_differential(omega_b + 0.5*dt*k2, quaternion + 0.5*dt*l2)
l4 = quaternion_differential(omega_b + dt*k3, quaternion + dt*l3)
new_omega_b = omega_b + 1/6 * (k1 + 2*k2 + 2*k3 + k4) * dt
new_quaternion = quaternion + 1/6 * (l1 + 2*l2 + 2*l3 + l4) * dt
new_quaternion = new_quaternion / np.linalg.norm(new_quaternion)
return new_omega_b, new_quaternion
def calculate_rotation(omega_b_init, frame_b_init, inertia_cog, dt, total_step):
inertia_inv = np.linalg.inv(inertia_cog)
time = np.arange(total_step) * dt
frame_b = np.zeros((3,3,total_step), dtype=float)
omega_b = np.zeros((3,total_step), dtype=float)
frame_b[:,:,0] = frame_b_init
omega_b[:,0] = omega_b_init
for i in range(total_step-1):
omega_b[:,i+1], frame_b[:,:,i+1] = runge_kutta(omega_b[:,i], frame_b[:,:,i], inertia_cog, inertia_inv, dt)
return time, omega_b, frame_b
def calculate_rotation_quaternion(omega_b_init, quaternion_init, inertia_cog, dt, total_step):
inertia_inv = np.linalg.inv(inertia_cog)
time = np.arange(total_step) * dt
quaternion = np.zeros((4,total_step), dtype=float)
omega_b = np.zeros((3,total_step), dtype=float)
quaternion[:,0] = quaternion_init
omega_b[:,0] = omega_b_init
for i in range(total_step-1):
omega_b[:,i+1], quaternion[:,i+1] = runge_kutta_quaternion(omega_b[:,i], quaternion[:,i], inertia_cog, inertia_inv, dt)
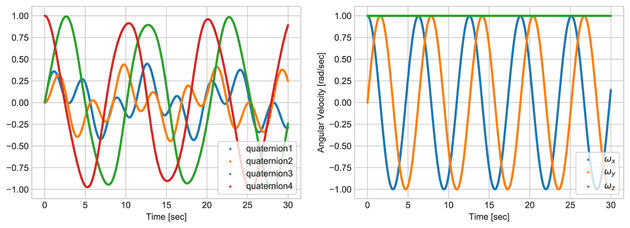
return time, omega_b, quaternion剛体回転の例題
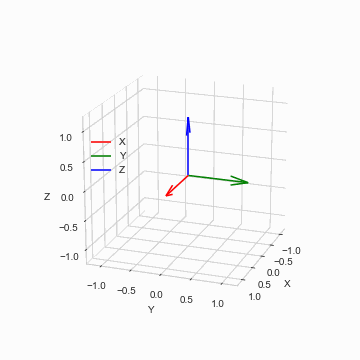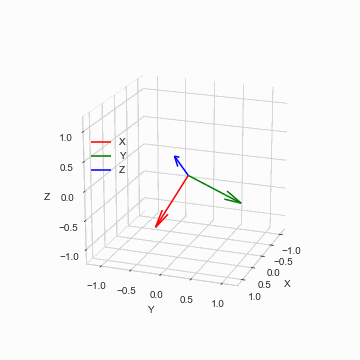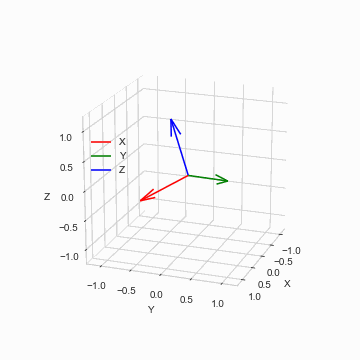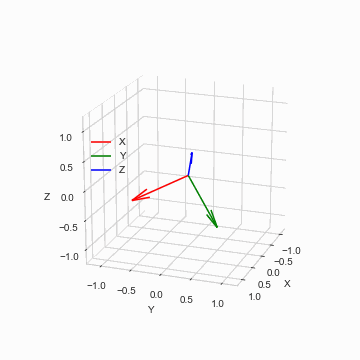
実際に何かシミュレーションするには，これに回転させたいものの質量特性と，姿勢・角速度の初期条件を与えてやればよい．シンプルなケースとして，物体の慣性モーメントと初期角速度を次のように取る．
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
import matplotlib.animation as animation
import numpy as np
from rigid_body import inertia_conversion
from rigid_body import calculate_rotation_quaternion
from rigid_body import quaternion2dcm
from mpl_toolkits.mplot3d import Axes3D # noqa: F401 unused import
plt.rcParams["font.size"] = 12
mass = 10.0
inertia = np.array([[1.0, 0.0, 0.0],
[0.0, 1.0, 0.0],
[0.0, 0.0, 2.0]])
cog = np.array([0, 0, 0])
dt = 0.01
inertia_cog = inertia_conversion(mass, inertia, cog)
total_step = 3000
omega_b_init = np.array([1.0, 0.0, 1.0])
quaternion_init = np.array([0.0, 0.0, 0.0, 1.0])
time, omega_b, quaternion = calculate_rotation_quaternion(omega_b_init, quaternion_init, inertia_cog, dt, total_step)
dcm = np.zeros((3,3,total_step), dtype=float)
for i in range(total_step):
dcm[:,:,i] = quaternion2dcm(quaternion[:,i])
vec_x = dcm[0,:,:]
vec_y = dcm[1,:,:]
vec_z = dcm[2,:,:]
fig1 = plt.figure(figsize=(12, 4))
ax = fig1.subplots(1,2)
ax[0].scatter(time, quaternion[0,:], s=2, label='quaternion1')
ax[0].scatter(time, quaternion[1,:], s=2, label='quaternion2')
ax[0].scatter(time, quaternion[2,:], s=2, label='quaternion3')
ax[0].scatter(time, quaternion[3,:], s=2, label='quaternion4')
ax[0].set_xlabel('Time [sec]')
ax[0].legend(loc='lower right', frameon=True)
ax[1].scatter(time, omega_b[0,:], s=2, label='omega_x')
ax[1].scatter(time, omega_b[1,:], s=2, label='omega_y')
ax[1].scatter(time, omega_b[2,:], s=2, label='omega_z')
ax[1].set_xlabel('Time [sec]')
ax[1].set_ylabel('Angular Velocity [rad/sec]')
ax[1].legend(loc='lower right', frameon=True)
filename = 'rotation' + '.pdf'
fig1.savefig(filename, format='pdf', dpi=1000, bbox_inches='tight', pad_inches=0.1)
fig2 = plt.figure(figsize=(5, 5))
bx = fig2.gca(projection='3d')
def update(i):
num = i * 15
bx.cla() # clear plot
bx.view_init(elev=20, azim=20)
x = np.zeros(3, dtype=float)
y = np.zeros(3, dtype=float)
z = np.zeros(3, dtype=float)
u = np.array([vec_x[0,num], vec_y[0,num], vec_z[0,num]])
v = np.array([vec_x[1,num], vec_y[1,num], vec_z[1,num]])
w = np.array([vec_x[2,num], vec_y[2,num], vec_z[2,num]])
bx.set_xlim([-1.2,1.2])
bx.set_ylim([-1.2,1.2])
bx.set_zlim([-1.2,1.2])
bx.set_xlabel('X')
bx.set_ylabel('Y')
bx.set_zlabel('Z')
bx.quiver(x[0], y[0], z[0], u[0], v[0], w[0], color='r', label='X')
bx.quiver(x[1], y[1], z[1], u[1], v[1], w[1], color='g', label='Y')
bx.quiver(x[2], y[2], z[2], u[2], v[2], w[2], color='b', label='Z')
bx.legend(loc=[0.15,0.5])
ani = animation.FuncAnimation(fig2, update, frames = 200)
ani.save('rotation.gif', writer='pillow')今回のケースは，オイラーの運動方程式（剛体の運動方程式を参照）に代入してやれば，角速度の時間発展がとなることがすぐに分かる．実際，角速度のグラフはZ軸が一定，XY軸が振動して，予想通りの結果になっている．一方，クオータニオンの方は正直グラフを見ても，何がなんだか分からないので，クオータニオンから座標の基底ベクトルに変換して，座標の変化をアニメーションにしてみた．（細かいことは調整していないのでアニメーションの早さ等は適当．）
Left: Orientation in Quaternion, Right: Evolution of Angular Velocity
TASIndex - Spacecraft Thermal Analysis Database
A comprehensive database of spacecraft thermal analysis information and software for flight missions.
Psychroid - Psychrometric Chart Calculator
Interactive psychrometric chart calculator for HVAC engineers. Calculate and visualize air properties, process flows, and energy requirements.
Craftbook - Spacecraft Thermal Engineer's Notebook
Technical articles on thermal and aerospace engineering topics, featuring mathematical derivations and code examples.
View Factor Calculator
Radiation view factors (configuration factors) for different geometrical configurations are calculated by the analytical formula and Monte Carlo method.